|
Math 535 Measure Theory
|
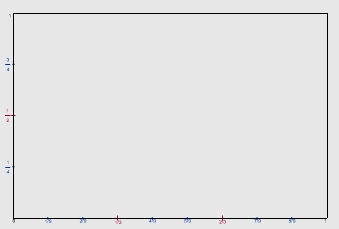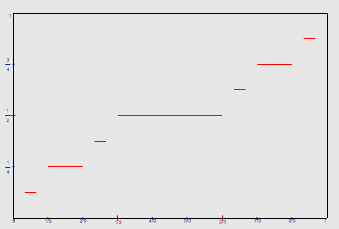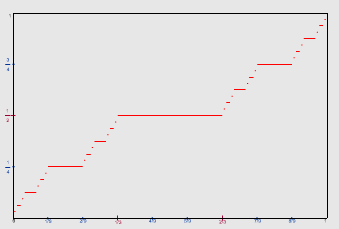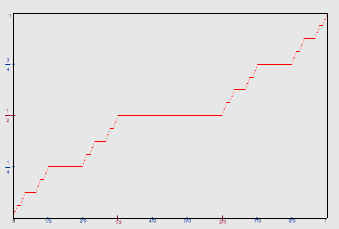
Click the image to display a Cantor function plotter. |
|
Current Downloads
Tips for the final: Tips for Exam 1 and Tips for Exam 2 posted previously apply. The Final will also include the part of the material covered after the part included in Exam 2 up to Lp spaces (not including Lp spaces.) Study your notes for that part. See you next week! Tips for Exam 1 Tips for Exam 2 fn converges to f in measure but not a.e. -- an animation (Just for fun.) Class 23 -- PDF Notes Class 23 -- Video Part 1 Class 23 -- Video Part 2
Homework 1 -- Selected Solutions
Homework 2 -- Selected Solutions
Homework 6 -- Selected Solutions Homework 7 -- Selected Solutions Homework 8 -- Selected Solutions Homework 9 -- Selected Solutions A proof of the Egoroff Theorem -- Video A proof of the Egoroff Theorem -- PDF Description of the Course In this course, we shall explore the heart of real analysis: Lebesgue measure, the Lebesgue integral, convergence theorems, the classical Banach spaces, and other exciting topics. Exams and Evaluation Your grade will be based on exams, homework, and class participation. We shall discuss grading during the first class. We will decide together how many exams to have and how to schedule them. See you in class!
|
![]()
|
Page last modified: December 14, 2006 |
Math Home | URI Home |
