Exponential Decay - Example

Problem:   A radioactive isotope of iodine decays exponentially. There is 50 mg of the element initially, 35 mg after 4 days.

      (a) Find a formula of the form

R(t) = R[0]*exp(-k*t)

       that models the process of decay.

      (b) Find the half-life, t[h] , of the isotope.

As we found out, the formula decsribing the decay is

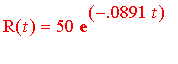R(t) = 50*exp(-.891e-1*t) .

Half-life is the time, t[h] , after which half of the initial amount of 50 mg decomposes, and 25 mg is left. Hence, to find t[h] we have to solve for t[h] the equation

25 = 50*exp(-.891e-1*t[h]) .

We divide both sides by 50, and take the natural logarithm of both sides. We obtain

ln(25/50) = ln(exp(-.891e-1*t[h])) .

Since ln(exp(-.891e-1*t[h])) = -.891e-1*t[h] (from properties of logs), we get

-.891e-1*t[h] = ln(1/2) .

Hence, the half-life is

t[h] = ln(1/2)/(-.891e-1) .

The latter gives the half-life t[h] = 7.78 days, approximately. As we know, that means that half of the amount will be gone after 7.78 days; after the next 7.78 days half of what's left will be gone again, and so on.