Exponential Decay - Example

Problem:   A radioactive isotope of iodine decays exponentially. There is 50 mg of the element initially, 35 mg after 4 days.

      (a) Find a formula of the form

R(t) = R[0]*exp(-k*t)

       that models the process of decay.

      (b) Find the half-life, t[h] , of the isotope.

We know already that our formula is

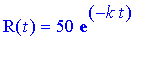R(t) = 50*exp(-k*t) .

To find k , we use the fact that after 4 days, that is, at t=4 , there are 35 mg of iodine left. That gives us the following equation

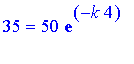35 = 50*exp(-k*4) .

We divide both sides by 50, and take the natural logarithm of both sides. We obtain

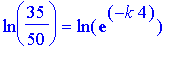ln(35/50) = ln(exp(-k*4)) .

Since 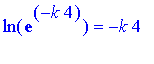ln(exp(-k*4)) = -k*4 (from properties of logs), we get

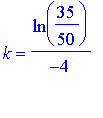k = ln(35/50)/(-4) = 0.0891 .

Hence, the formula describing the decay of iodine is

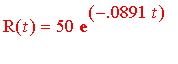R(t) = 50*exp(-.891e-1*t) .