
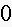 to
to

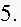 The
density function of the scores is shown in the figure below.
The
density function of the scores is shown in the figure below.
Fall 2004
Practice Exam 2
Instructor: M. Kulenović
Kingston 10/10/2004
1.
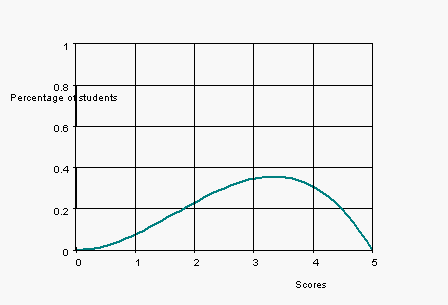
An exam given to a large number of students is
scored from

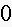 to
to

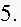 The
density function of the scores is shown in the figure below.
The
density function of the scores is shown in the figure below.
Estimate the percentage of students scoring between

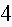 and
and

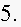
Estimate the percentage of students scoring less than

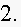
Estimate the median and the mean.
2. The density function for the
lifetime for certain type of switching device is shown in the figure below.
The time

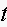 is
measured in months and
is
measured in months and

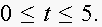
Estimate the percentage of switching devices which lifetime is between

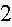 and
and

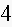 months
months

Estimate the percentage of switching devices which lifetime is less than

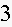 months.
months.
Estimate the mean and the median value of this switching device.
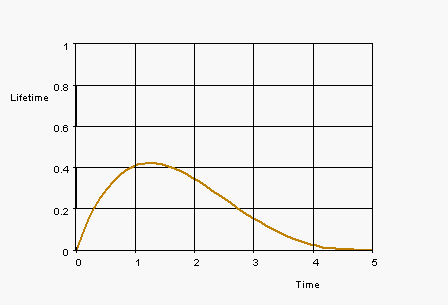
3. Given the following probability density function:

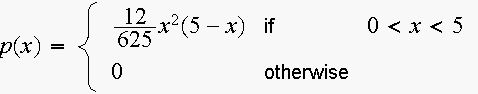
Find its cumulative distribution function.
Find its mean value and the median.
4. Match the graphs of surfaces to the equations. Explain.
(a)

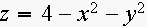 (b)
(b)

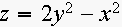 (c)
(c)

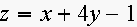
(i)
 (ii)
(ii)
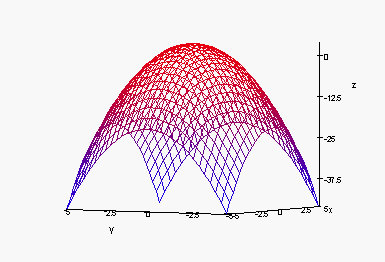
(iii)
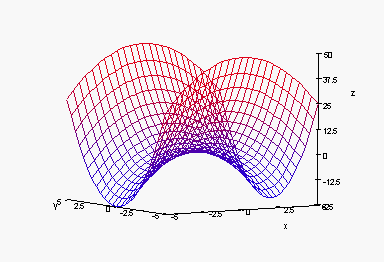
5. Match the contour diagrams to the equations in the previous problem. Explain.
(i)
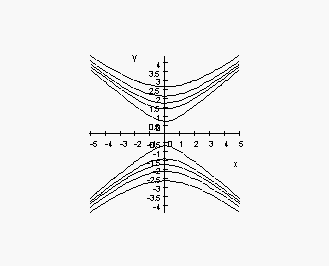 (ii)
(ii)
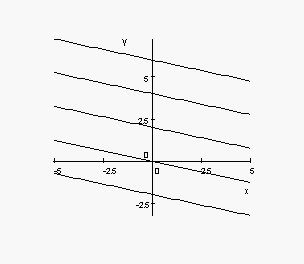
(iii)
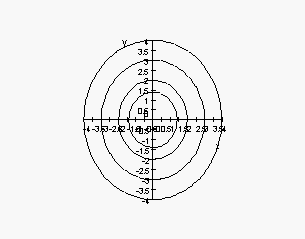
6. Fill in the blanks in a partial table of values for a linear function:
 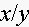 |
 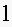 |
 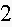 |
 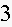 |
 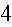 |
 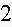 |
 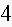 |
 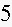 |
||
 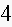 |
 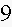 |
 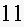 |
||
 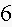 |
||||
 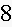 |
||||
Find an equation for this linear function.
7. Consider
the function

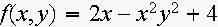
(a) Estimate

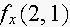 and
and

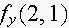 from a table of values for
from a table of values for

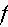 with
with

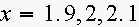 and
and

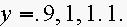
(b) Compare the estimates in part (a) with the exact
values of

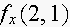 and
and

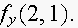
8. Suppose
that your weight

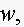 in pounds, is a function
in pounds, is a function

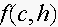 of the number
of the number

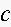 of
calories you consume daily and the height
of
calories you consume daily and the height

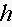 in inches. Using units, interpret, in everyday terms the statements:
in inches. Using units, interpret, in everyday terms the statements:
(a)

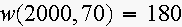 (b)
(b)

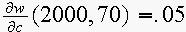
(c)

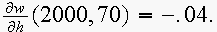
Estimate

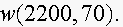
9. Find all critical points of the function:

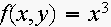

Determine if the critical points are local maxima, minima, saddle points, or none of these.
10. Design a rectangular milk carton box of width

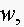 length
length

 and height
and height

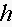 which holds
which holds

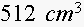 of milk. The sides of the box cost
of milk. The sides of the box cost

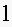 cent/
cent/
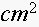 and the top and bottom cost
and the top and bottom cost

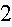 cent/
cent/
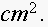 Find the dimensions of a box that minimize the total cost of materials used.
Find the dimensions of a box that minimize the total cost of materials used.
11. Consider data points

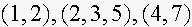 .
Suppose you want to find a least square line
.
Suppose you want to find a least square line

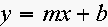 for these data points without using a calculator program. What function
for these data points without using a calculator program. What function

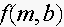 should be minimized ?
should be minimized ?