MATH 244/1

URI/Spring 2004

Instructor: Prof. M. Kulenović

Maple Project
Due date: March 1, 2005

                                                                                                                                                                                                           Kingston, 2/15/2005

The objective of this project is to use Maple's symbolic manipulation capabilities to solve certain differential equations and to use Maple's graphics capabilities to plot the required solutions of these equations.

Use Maple's worksheet that you will find in:

http://www.math.uri.edu/~kulenm/m244sp05

1. Consider the exact differential equation:

(x2 y + 2 sin(2x+y) - e2x y) dx + (x3 /3 + sin(2x+y) - e2x /2) dy = 0.
(a) Find the general solution of this equation by using dsolve command.

(b)  Use dsolve command to find the particular solutions of this equation that satisfies the initial conditions  y(0) = 1 and y(0) = -2.
(c)  Plot the obtained solutions along with the direction field.

2. Consider the Bernoulli's differential equation:

x y' + 2 y =  x2  cos(x2 ) y-1 .
(a) Find the general solution of this equation by using dsolve command.

(b) Use dsolve command to find the particular solutions of this equation that satisfies the initial conditions  y(1) = -1 and y(1) = 4.

(c)  Plot the obtained solutions along with the direction field.

(d) Use Maple to perform the substitution w = y2 and transform the initial equation into linear differential equation.

3.
(a)   Use Abel's formula

MATH
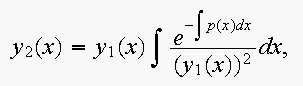
and Maple to find a second linearly independent solution of the following differential equation with the given solution:
(2 cos (x) + sin (x) ) y'' - 5 cos (x) y' + (2 cos(x) - 4 sin(x) ) y = 0
y1(x) = cos(x).

(b)  Use dsolve command to find the particular solution of this equation that satisfies the initial conditions

y(0) = 1, y'(0) = 2.


(c)   If dsolve command does not work use (a) to find the solution.