0
to 5
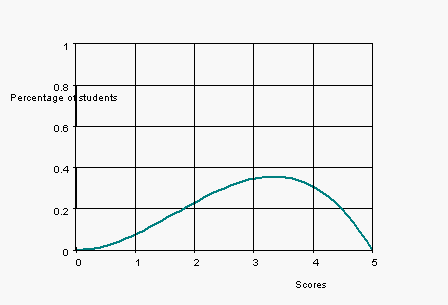
The
density function of the scores is shown in the figure below.
Fall 2005
Practice Exam 2
Instructor: M. Kulenović
Kingston 10/10/2005
1.
An exam given to a large number of students is
scored from
0
to 5
The
density function of the scores is shown in the figure below.
Estimate the percentage of students scoring between
2
and
5
Estimate the percentage of students scoring less than
3
Estimate the median and the mean.
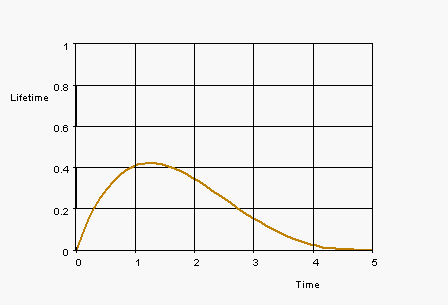
2. The density function for the
lifetime for certain brand of light bulbs is shown in the figure below.
The time
t
is
measured in months and
0
< t < 5.
Estimate the percentage of light bulbs which lifetime is between
1 and
4
months
Estimate the percentage of light bulbs which lifetime is less than
2
months.
Estimate the mean and the median value of the light bulbs.
3. Given the following probability density function:
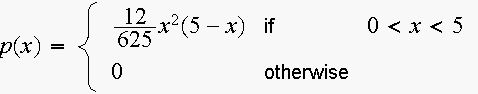
Find its cumulative distribution function.
Find its mean value and the median.
4. Match the contour diagrams to the equations. Explain.
(a) z
= 4 - x2 - y2
(b) z
= 2y2 - x2
(c) z
= x + 2y - 1
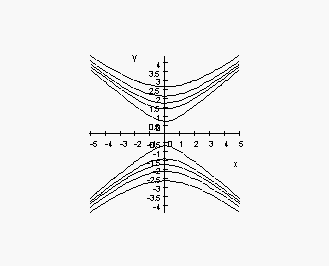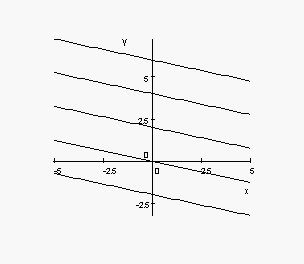(i)
(ii)
(iii)
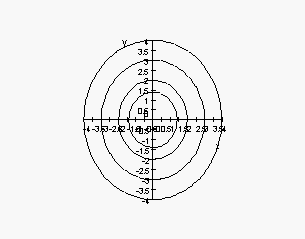
5. Fill in the blanks in a partial table of values for a linear function:
| x/y | 1 |
2 |
3 |
4 |
| 2 |
11 |
9 |
||
| 5 |
11 |
7 |
||
| 8 |
||||
| 11 |
Find an equation for this linear function.
6. Consider
the function
f (x, y) = 4 x - x2 - x y2
(a) Estimate fx
(1, 2) and
fy
(1, 2) from a table of values for
f
with
x = 0.9, 1, 1.1 and
y
= 1.9, 2, 2.1.
(b) Compare the estimates in part (a) with the exact
values of
fx
(1, 2) and
fy
(1, 2).
7. Suppose
that your weight
w
in pounds, is a function
f
(c, h) of the number
c of
calories you consume daily and the height
h
in inches. Using units, interpret, in everyday terms the statements:
(a) w(2000,
71)= 190
(b) wc(2000,
71)= 0.07
(c)
wh(2000,
71)= - 0.05
(d) Use the linear approximation formula to
estimate
w(2100,
72).
8. Find all critical points of the function:
f (x, y) = 4 x - x2 + 2y - x y2
Determine if the critical points are local maxima, minima, or none of these.
9. Design a rectangular milk carton box of width
w
length
l
and height
h
which holds
1024
cm3 of milk. The sides of the box cost
2
cent/cm3
and the top and bottom cost
4
cent/cm3
Find the dimensions of a box that minimize the total cost of materials used.
10. Consider data points
(1,
2), (2, 5), (4,7).
Suppose you want to find a least square line
y
= m x + b for these data points without using a calculator program. What function
f (m, b)
should be minimized ?