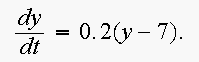
Fall 2004
Practice Exam 3
Kingston 11/12/2004
1. (a) Find the general solution to the differential equation
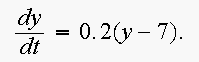
(b) Solve the initial value problem
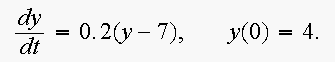
2. Consider the following functions:
(a) 
(b) 
Which of them is a particular solution to the differential equation
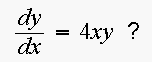
Which of them is a solution to the initial value problem
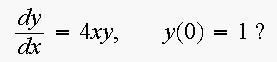
3. A population of insects at time 
, 
increases at a rate
proportional to the size of the population, with the coefficient of
proportionality 
The
time 
is
measured in hours.
(a) Write a differential equation for the
function 
(b) Find the general solution to this equation.
(c) If the initial population is 
, how
many insects will be present after 
hours ?
4. Suppose that at 
am
one winter morning, there is a power failure at your house in Vermont,
and your heat does not work without electricity. When the power goes
out, it is 
in your house. At 
pm,
it is 
in the house, and you notice that it is 
outside.Assume that Newton's Law of Cooling applies to the temperature 
in
your home.
(a) Write a differential equation
satisfied by the temperature, 
.
(b) Solve the differential equation and
estimate the temperature in the house when you get up at 
am
the next morning.
5. The amount of a drug in a patient's
bloodstream, 
, in 
,
decreases at a rate proportional at each instant to the amount of the
drug present with the coefficient of proportionality 
.
The time 
is
measured in hours.
(a) Write a differential equation for the
function 
.
(b) Find the general solution to the equation.
(c) If the initial amount 
,
how much drug is left after 
hours ?
6. The following system of differential equations represents the interaction between two populations, x and y.
 |
 |
(a) Describe how the species interact. Are they helpful or harmful to each other ?
(b) Write a differential equation for 
7. A radioactive isotope is released into the air as an
industrial by-product. This isotope is not very stable due to
radioactive decay. Two-fifths of the original radioactive material
loses its radioactivity after each month. If 
grams
of this isotope are released into the atmosphere at the end of the
first and every subsequent month, then
(a) how much radioactive material is in the atmosphere at the end of the tenth month?
(b) In the long run, i.e., if the
situation goes on forever, what will be the amount of this radioactive
isotope in the atmosphere at the end of each month ?
8. Each day at noon a hospital patient receives 
of a
drug. This drug is gradually eliminated from the system in such a way
that over each 
hour
period the amount of the drug from the original dose is reduced by 
. On
the other hand, the patient is receiving a new 
dose each day.
(a) How much of the drug is present in the
patient's system immediately after noon on the 
-th day
of treatment ?
(b) If the regime is continued
indefinitely, at what level will the amount of the drug in the
patient's system stabilize, measured immediately after noon every day ?
9. Use geometric series to find simple fractions that equal the following repeating decimals:
(a) 
(b) 
10. At the end of year 
,
world oil reserves were about 
billion barrels. During 
,
about 
billion barrels of oil were consumed. Over the past decade, oil
consumption has been increasing at about 
per
year
.
(a) Assuming oil consumption increases at this rate in the future, how long will the reserves last ?
(b) Assuming oil consumption increases at
the rate of 
per
year in the future, how long will the reserves last ?
This document created by Scientific Notebook 4.0.